Simplified Sequential Dutch Auctions
Sequential Dutch Auctions (SDA) are the backbone of Olympus-style bonds. Bond Protocol is a permissionless auction system for exchanging tokens using SDA and other auction mechanics. I've worked on systems related to these auctions for a year and a half now and authored a research paper on the original SDA mechanism last year. That paper was a bit dense and inaccessible to many. The reason was I could not explain a dynamic system simply. Specifically, the original system behaves more like an industrial control system than a well-specified math model. More recently, I designed a simplified version of the SDA mechanism for our Oracle-based auctioneers, called OSDAs, which does not use tuning. In doing so, I was able to break away from some previously conceived notions that were connected to tuning. As a result, here is a more succinct, simpler model to understand SDAs.
Goal of an SDA
SDAs seek to sell out the capacity of the market evenly (linearly) over the duration. Capacity can be defined in either the token you want to buy or sell, but the math is the same in either case. The important thing is that the market is going to try to sell out the whole capacity, regardless of whether the external market prices of each token go up or down. The "tuning" version of SDAs seeks to ensure this happens by adjusting its price with market movements, but "non-tuning" versions simply expect external market prices will stay relatively close to the start price. Otherwise, capacity will sell out early (if the external price goes up) or won't completely sell out (if the external price goes down). The version explained in this article is "non-tuning". The following chart shows a notional SDA market:
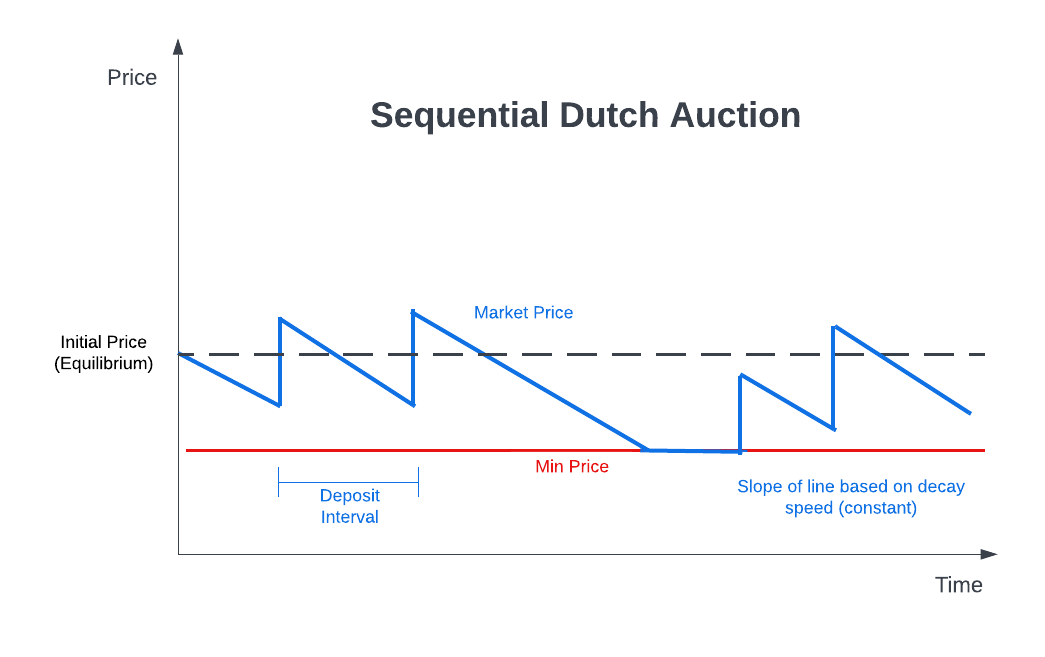
This is comparable to other time-based sale mechanisms such as Paradigm's Gradual Dutch Auctions (GDA) and Time-Weighted Automated Market Makers (TWAMM). The new version of SDAs is most similar to the Paradigm Continuous GDA version. The main difference between SDAs and GDAs is how they break capacity up during the market duration.
SDA
SDAs break capacity into a set of discrete chunks that can each be at most a certain percent of the total capacity (max payout). Users can buy one of these variable-size chunks at a time at the current discount. In practical terms, this means users can buy up to the max payout at the current discount on an SDA.
GDA
GDAs break capacity into infinitesimal chunks over the duration and auctions them off separately. Users can buy as many chunks as are remaining, but each chunk has a different discount (extending to a premium if the "auction" for the next chunk hasn't started yet). In practical terms, this means that the discount received on a GDA purchase goes down as the number of tokens purchased increases. This is similar to "negative price impact" on an AMM, but the formula depends on the decay curve used by the auction.
Capacity vs. Time
Since the goal of an SDA is to evenly sell out capacity over time, we can measure whether it is on track at any point in time by comparing the actual capacity with the expected capacity then. If the actual capacity is less than the expected capacity, the market has oversold and the price should be higher, and vice versa. Therefore, a key value in our equation is the "capacity ratio".
The expected capacity is determined by the percent of the market duration that has elapsed. We calculate it as:
$$\chi(t) = C_0 \times \frac{L - t}{L}$$
where \(t\) is the current time, \(L\) is the length (duration) of the market, and \(C_0\) is the initial capacity of the market.
(Side note: Expected capacity decreases linearly here as defined in the goal of the SDA, but we could easily create different issuance curves such as logistic or exponential by adjusting this function, similar to Paradigm's VRGDAs)
We calculate the capacity ratio as:
$$r(t) = \frac{\chi(t) - C(t)}{C_0}$$
where \(C(t)\) is the remaining capacity at the time \(t\), \(\chi(t)\) is the expected capacity, and \(C_0\) is the initial capacity of the market as defined above.
Equilibrium Price
In a standard non-tuning SDA, the starting price of the market is the "equilibrium price" for the decay mechanism, meaning that if actual capacity and expected capacity are equal at a given point in time, then the price should be the start price. We'll call this equilibrium price \(P_0\).
Decay Speed
Now that we have a capacity ratio, we know if the market price should be higher or lower than the equilibrium price at any given moment. However, how much higher or lower should it be?
The existing "tuning" SDAs use a concept called a "debt decay interval" to determine the speed of price dropping. A debt decay interval of 5 days means that it should go from the most recent reset value to zero in 5 days, or 20% per day.
We can use a similar concept here. Both versions use a target "deposit interval" to set the maximum purchase size for a market. If you have a market that is 5 days long and the deposit interval is 1 day, then the maximum purchase is 20% of capacity (1 / 5 = 0.2). In a perfect world, purchases would be made exactly on schedule at this interval at the max size. Therefore, as the seller, what discount do I think a buyer would accept to purchase that amount on schedule? We call this the "target interval discount". Depending on how high or low it is, the market will need to decay faster or slower. Therefore, we calculate the decay speed as:
$$k = \frac{L}{I_d} \times d$$
where \(L\) is the duration of the market, \(I_d\) is the deposit interval, and \(d\) is the target interval discount.
Market Price
We can now combine these concepts to derive our market price equation:
$$P(t) = P_0 \times (1 + k \times r(t))$$
where \(P_0\) is the equilibrium price, \(k\) is the decay speed, and \(r(t)\) is the capacity ratio.
Application to OSDAs
The Oracle-based Sequential Dutch Auction (OSDA) combines the benefits of this simplified pricing model with the adjustment of a "tuning" version. Specifically, the oracle price becomes the "equilibrium price" so the auction always has an up-to-date reference point. The Bond Protocol implementation allows specifying a base discount from the oracle price. Market makers may want to do this if they are requiring a longer vesting duration on the payout since the present value of that vesting token may be lower than the market price of the underlying. We modify the price equation slightly based on the new equilibrium price:
$$P(t) = O(t) \times (1 - b) \times (1 + k \times r(t))$$
where \(O(t)\) is the oracle price at time \(t\), \(b\) is the base discount percent of the market, \(k\) is the decay speed, and \(r(t)\) is the capacity ratio.
The following chart shows a notional OSDA market:
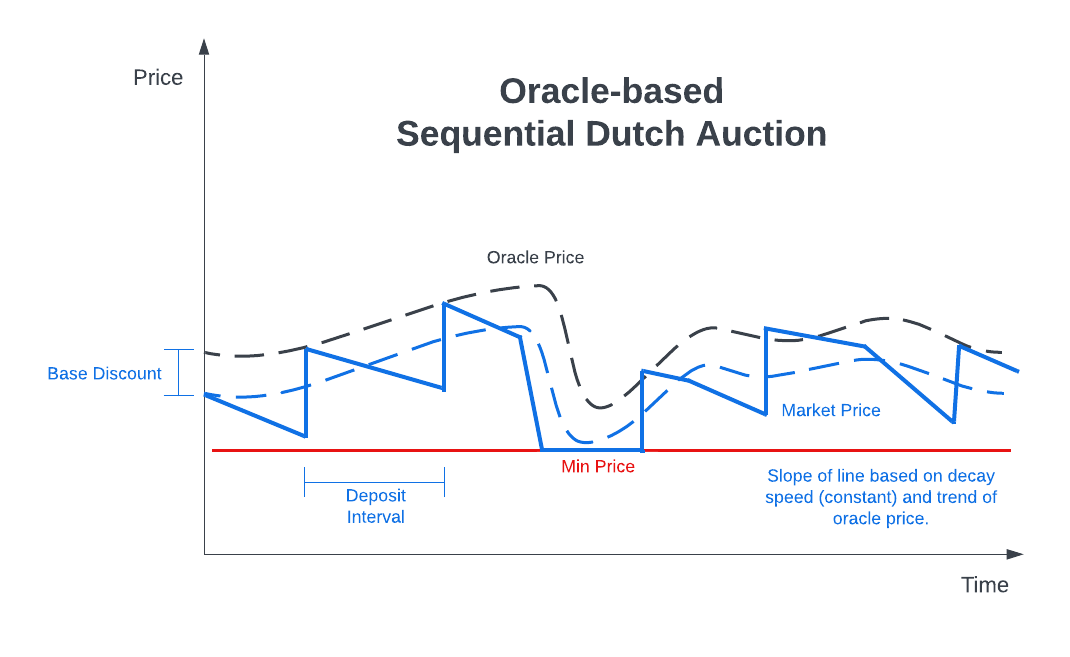
Market creators can also set a minimum total discount from the starting price, which creates a hard floor for the market price and limits selling during a market crash.
Configuring appropriate base and target interval discounts is a function of the market demand for the token and the vesting period of the payouts. Typically, longer vesting periods require a larger base discount. Target interval discounts may need to be higher for smaller cap tokens or where demand is soft. However, various combinations can be used depending on desired market characteristics. For example, a high base discount and low target interval discount will give a consistently good deal with low volatility in the market price. The opposite configuration, low base discount and high target interval discount, will be more volatile, but may result in lower overall discounts depending on demand.
Conclusions
The necessary complexity of auction mechanisms varies greatly depending on the use case. The original SDA design was meant to service a wide range of market environments and auction durations. While useful, the tuning behavior of these markets can sometimes be suboptimal and simpler versions can provide more predictable behavior when that is all that is required. An example would be very short-duration markets where the external market prices of the payout and quote tokens aren't likely to change much. Additionally, while oracles have their downsides, OSDAs provide an alternative for longer-duration markets for tokens that have reliable on-chain oracle feeds while leveraging a simpler mechanism.